x^{p−2} ̸≡ z^{p−2} mod δ
x^{p−2} ̸≡y^{p−2} mod δ
z^{p−2} ̸≡ y^{p−2} mod δ
ではありますが、前回の論文では「δ = θR1 に属する。」としながらも
きちんとδを導出できていなかった部分があったため
追記修正しました。
タイトル変わりましてバージョン1となります。
年を取ったなと思うこと
最近、仕事から帰り最低限の用事を済ますと2時間起きているのが限界。
できることなら猫のようにゴロゴロとしていたいものです。
フェルマーの最終局面35
理解が不十分なところがあり、前回の記事で見かけの配置と書いてたのは実体【Actual conditions】でした。【General solution conditions】は同値変換の成立条件が共通の場合に変換できるという位置づけになります。同値変換の成立条件が共通である場合、3組全て成り立つか成り立たないかどちらかになり、それに基づいて展開してます。
フェルマーの最終局面34
バージョン3での不備はz^{p-1}/≡y^{p-1}かつ-z/≡yのとき
x^p+yz^{p-1}≡zy^{p-1}では評価できない事です。条件の漏れが出てしまいました。
主力としていた解の条件が使えないので「もうだめぽ。。」と思ったわけです。
最終局面31に書いたのですが、≡である条件は特定できるものですが、/≡は取り扱うのが難しいです。
そこで解の条件を拡張して一般(式の)解の条件(General solution conditions)を得ようと考えました。
一般式であるならば「≡」ではないものは全て「/≡」と言えるからです。
とは言っても、どうしたら一般式を得られるのか分からず大きい障壁でした。
U≡-ｚ、T≡-ｙとしたところで何もわかりませんし。。(´・ω・`)
以前考えていた同値変換が使えないかと模索してたのですが、しばらく使い方が見いだせなかったです。
x^p,y^p,z^pまでs1、t1、u1で変数で表すことで、General solution conditionsについて見えてきました。
solution conditionsでは入力値に制限があったのですが、General solution conditionsは汎用な同値変換から任意の条件を設定して得られるものです。またsolution conditionsでは演算によってx^p、y^p、z^p項の2項が得られますが、General solution conditionsは同値変換の成立条件で対応させます。矢印は2項入れ替えで第一式がx^p、y^p、z^pと成りうる2パターン示しています。下図は見かけの配置であり、実体はGeneral solution conditionsの配置です。まだx^p、y^p、z^pの2項は数式上の対応はしてないので(≡と/≡)共通で確定してます。
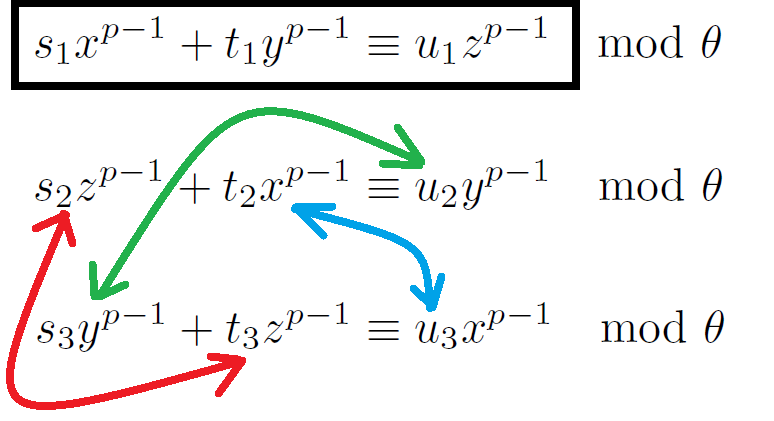
最終局面29でR条件と捉えたのは間違いかと思って一旦は破棄したものですが復活させました。
なので過去の論文にいくらか追記した感じです。(L条件、R条件の定義は安定しないため辞めました。)
フェルマーの最終局面33
使えそうなものがあったのですが、概念の理解に時間が掛かりそうです。
1+1＝2くらい簡単なものなのですが、このあたり頭が四角いせいか数日間理解できません。
フェルマーの最終局面32
LとRコンディションがともに成り立たない部分が評価できてないと思いました。
次の手が思いつかない。もうだめぽ。。
フェルマーの最終局面31
理詰めが浅かったようなので追記修正しました。
解の条件2は不要かもしれないですが、もう一つの見方として記述してます。
例えば5個のボールがあり各番号が書いてあるとします。
「2のボールである。」なら2のボールと特定できますが
「2のボールでない。」なら1、3、4、5の何れかでありますが特定できません。
ただし、2個のボールであれば「2のボールでない。」なら1のボールであると特定できます。
3/5追記
Condition LとRが成り立たない仮定の説明は
単純にx^p+y^pとz^pが合同にならないだけで良かったのかもしれません。(´・ω・`)？
フェルマーの最終局面30
フェルマー最終定理の考察について自然にフェードアウトしてたのですが、
数日前にモヤモヤしたものが残っているのを思い出して、
ブランクにより俯瞰的に気づくこともあるだろうと再チェックしたところ不備が見つかりました。
それは解の条件でyz ≡ UT mod θであればxp + yp ≡ zp mod θを満たすという部分です。
合同式というのは例えば4を法とすれば5、9、13・・・は合同で多価でありますが
だからといってyz ≡ UT mod θを満たす組み合わせ全てが互いに合同になるのは違和感があります。
ここがモヤモヤしていた部分だと考えたところ、原因は
前提条件xp + Uz＾p−1 ≡ Ty＾p−1 mod θで合同式を満たしていなければならないことを確認してませんでした。
つまりyz ≡ UT mod θを満たす組み合わせ全てが、この合同式を満たしているとは限らないと考えれば先のモヤモヤは解消されます。
その件について修正しました。
latexの参照が一致しないとき
いくら探してもLatexの参照が一致しなかったのですが、ようやく直りました。
備忘録として書いておきます。
◆一致しなかったとき
\begin{eqnarray}
a+b=C\nonumber\\
a+b=C\nonumber\\
\label{1-2}
a+b=C\nonumber\\\nonumber
\end{eqnarray}
◆一致したとき
\begin{eqnarray}
a+b=C\nonumber\\
a+b=C\nonumber
\label{1-2}\\
a+b=C\nonumber\\\nonumber
\end{eqnarray}
フェルマーの最終局面29
今回の修正に関して：
x^p+y^p≡z^pが成り立つとき、同値変換が成り立ちます。
例えばL条件なら各行が合同となります。
R条件ではＬ条件の2項を入れ替えることで解の条件に対応すると考えていた(´・ω・`)のですが、
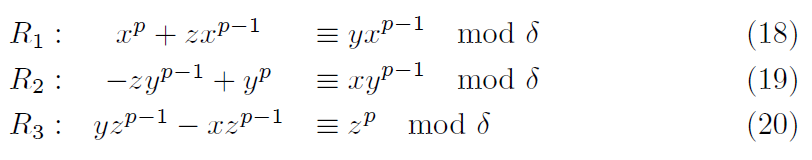
R条件が成り立つときにはL条件は成り立たない。つまりL条件の同値変換は成り立たないので、
ここで2項を入れ替えることは、解の条件に対して意味のない操作だと気が付きました。
また上式のRがx^p+y^p≡z^pとならないことが分かっても証明にはならないため、
修正しました。
shitetsuronnkou blog 