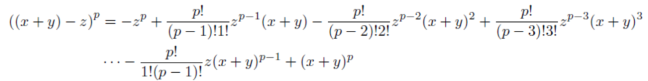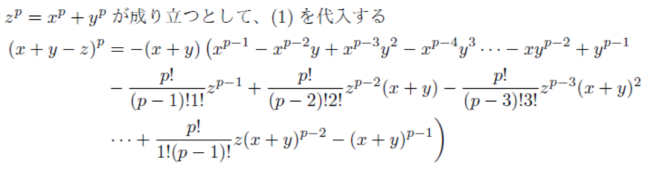フェルマーの最終局面3

デッドロックなので離れます。またいつか挑戦するかもしれないので備忘録を残して起きます。

私がこの命題でずっと悩ましいと感じているのは、恒等性です。つまり

文字式をこねくり回しているとA=Aのように当たり前の結果になってしまうことです。

それで証明の哲学を少し。

まず(a+b)^2=a^2+2ab+b^2のような恒等式があります。

命題が与えられると不定方程式が得られます。例えば

命題：(a+b)^2=2abとなる自然数は存在するか

解は

0=a^2+b^2

a^2=b^2

a=b であれば良い\\

仮に命題の不定方程式を命題不定方程式とします。

1.命題不定方程式ではその命題を解くことはできない。

と考えます。上記は命題の不定方程式で解けているように見えますが

(a+b)^2=2abとなる自然数が存在するならば、(a+b)^2=2abとなる自然数は存在する。

では解けていることにはならないという事です。

上記命題を解けるのは0=a^2+b^2と置いたためです。

これを仮に派生不定方程式とします。命題不定方程式を置くと派生的に得られるからです。

次に√2は無理数であるかという命題では

無理数でなければ有理数ということになるので√2=a/bと置けます。ここまでが命題不定方程式です。

両辺を2乗します。2=a^2/b^2これが派生不定方程式です。

フェルマーの最終定理では命題不定方程式は

x^n+y^n\=z^n (n>2)

派生不定方程式は例えば

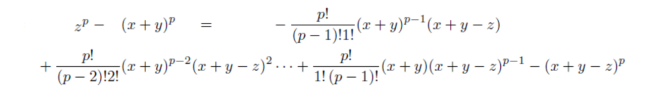
右辺がp^2の約数を持つので左辺もp^2の約数を持つ。

指数がp=3のときx,y,zのいずれかがpの約数を持つのは直ぐにわかります。3xy(x+y)

指数がp=5のときもx,y,zのいずれかがpの約数を持ちます。7以上はわかりませんでしたが・・

とりあえずx,y,zの文字式だけでは無理でも素数を使うことで何か判定することはできました。

ただ素数を使った代数的アプローチは十分に行われて駄目だったので、やはりx,y,zの文字式から

不定方程式を得られればと考えています。普通に考えれば恒等性が解消できそうにないですが

第五の演算を使ってから等号を結ぶようなことができれば不定方程式が得られるのではないかと思っています。

ただ、どのようにしたらいいのか見当がつきません。

 

フェルマーの最終局面2

最近の考察について述べます。

まず、二つの素数(奇数)の和に関する等式（The Barlow-Abel equations）があります。

これを以下の(x+y-z)^pの展開式へ代入します。

ワイルズ氏によりx^p+y^p=z^pが成り立たない事が示されたのですから以下の不定方程式に矛盾が出てきても良さそうですが・・・・。

約数について調べてみます。

しかし、全く矛盾を見つける事ができませんでした。（赤枠の部分は変形するとa,b,cの約数を持つ事が確認されました。）

二進も三進もいかない訳ですが、この理由について考えてみると以下の対応関係が成立している事に問題がありそうだと考えました。

z:(x+y)、y:(z-x)、x:(z-y)

x,yが奇数ならばzは偶数で正しく、x,yが互いに素ならばzは互いに素(上記参照：x+yが約数a,bを持つという流れにできない)であり他も同様です。

つまりz:(x+y)、y:(z-x)、x:(z-y)の対応関係が成り立っているという前提の下では偶奇性および互いに素により矛盾を得ることは無理そうです。

そのためz:(x+y)、y:(z-x)、x:(z-y)の対応関係が成り立っている事自体矛盾するといったアプローチへ変える必要があると考えました。

現状、きちんと理解していないのですが文字を交換する方法を試みています。