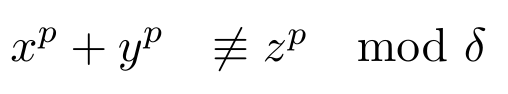フェルマーの最終局面15

正月のまったりできる時間が数日つぶれてしまい、会社が始まると何もできなくなりそうなので
時間を置いたのでフェルマーの最終定理バージョンzの検証と補足記事を書こうと思います。

fermat’s last theorem Vz　P.18　1.4 命題の条件について

読んでみたのだが、よくわかりずらかったので一旦忘れよう。

フェルマーの命題とは

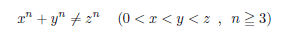
であり本来はノットイコールなのだが、ここではイコールとする。

それを合同式で表したものでθを法とするならばこんな感じ。

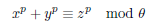
合同式ならばｘ，ｙ，ｚについて合同な別表現があるかもしれない。
それをフェルマーの命題条件と定義する。

式をいじくり倒した結果、2つで1セットのフェルマーの命題条件が得られました。

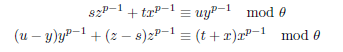
これら各項を選別してｓ、ｔ、ｕについての合同式をつくりますが
ｓ、ｔ、ｕの定義域はｓｔｕ≡ｘｙｚでなければなりません。

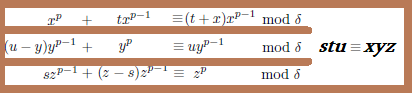
(25)において、ｔ≡ｚとしますが、ｕとｓについて自動的に導かれないのでｔΞｚはただ仮定しただけという事になります。
ｕΞｘ、ｓΞｙも仮定したところ特に競合とかなさそうです。ｕとｓが導出されないのは、上式の組み合わせが、そのような条件も含む弱いフェルマーの命題条件だからと考えられます。

そこでフェルマーの命題条件なら成立する1.3 解の条件を適用しｐ.20においてフィルタリングしてます。

すると以下の合同式を得ます。

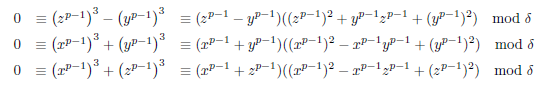
A^3-B^3≡(A-B)(3AB+(A-B)^2)
3ｚｙ⊥δ

であるからL⊥Ｒなので

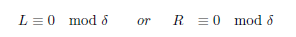
2回目の考察でフェルマーの命題条件を得ます。

ｘｙｚ⊥δが仮定にすぎないならば、矛盾があってもｘｙｚ|δの余地がまだ残りますが
ｘｙｚ⊥δは仮定ではないので強力な道具といった感じです。

電子は内側の軌道へ励起する？9

このテーマでの考察はゴチャってきた感があるのでコンパクトに再考し直そうと思います。

当初の疑問はマクロ系とミクロ系はどのように区別できるのであろうか？である。
小さい物理的事象を抽象的にミクロ系と位置づけているのか、明確に区別できるものなのか？

結論から言えばマクロ系とミクロ系の物理法則は相容れないとされているので後者であると考え話を進める。

それでマクロ系はミクロ系を構成単位として区別をするのである。
つまりマクロ系の構成単位の何かを0(または1)と位置づける。
繰り込みによりマクロ系で運動エネルギー0であってもミクロ系では運動エネルギーを有する(上図右)と考えることができる。
それをある種の位置エネルギーとするならば、どのような事が考えられるだろうか。
過去の記事では原子核を周回する電子のイメージに囚われていたために混沌としてしまった感があるので忘れる。

本記事では位置エネルギーを2つに大別してみよう。
一つは万有引力やクーロン力といった極座標としての位置エネルギー。もう一つは無向性の位置エネルギーである。

無向性の位置エネルギーの概念について仮定したものを説明する。
マクロ系ならば加速運動が大きいほど位置エネルギーが大きい(不安定)状態で、等速直線運動つまり停止が最もエネルギーが小さく0の(安定)状態である。
一方ミクロ系では加速度運動は常態化の系(量子ゆらぎ)であるため、量子ゆらぎより突飛な(量子ゆらぎに逆らうような外力を加えた)状態を位置エネルギーが大きいと考える。

そのため無向性の位置エネルギーは粒子の位置の軌道半径または領域を0に近づけるようとするほど大きな外力が必要になるだろうと仮定できる。不確定性原理を適用したいところだが概念から少々外れているようだ。

観測者効果(下左図)では観測手段より観測対象の運動エネルギーが大きいほど場の擾乱の影響が受けにくいというものであり、どちらかの運動エネルギーは固定した考察である。
観察者効果を考慮しない不確定性原理の考察　では補足となるが場の粒子(下右図緑丸)なるものがランダムに運動しているものをイメージし、一つだけオレンジに着色したとする。オレンジ粒子がおよそ定常な軌道であるならば、場の粒子の運動は系全体で等方的であり場の粒子は座標としての役割は大きくなり、非等方的なら運動エネルギーを齎す役割が大きくなる。この役割は100：0のように偏らないというものだろう。

よって不確定性原理というよりかは角運動量保存の法則的な考察に近い。

極座標としての位置エネルギーを考察すると粒子の運動エネルギーが小さくなると中心の方へ落ちてゆく。
ここに無向性の位置エネルギーを考慮すると粒子の位置の不確定性(軌道半径)を0に近づけるようとすると外力が必要となるため2つの位置エネルギーが釣り合うところで安定すると考えられる。

このために軌道半径が小さくなることをオレンジ粒子君が知っている必要がある。
これについてはミクロ系の運動はテンソルで記述されると仮定すると説明できそうである。
つまり、位置エネルギーが大きくなるとき(n+1)次の運動はn次の運動に基づいて形成されることで角運動量の成分(外力の情報)が保存されているという具合。

P≠NP予想の考察2

十分睡眠をとっても眠気が抜けない。
関節の怠さから精神的な無気力が生じているような気がする。屈伸やあくびは下等生物でも見られるので太古に形成されたDNAに何か関係あるのかもしれない…。このままでは何もしなくなるだろうという危機感からとりあえずキーボード一つ叩くことから始めて数ヶ月リハビリで記事を書く。(編集画面が新しくなっており非常に使いづらい)

pnp問題のv2を以前投稿をしたのでそれについて

探索者は答えを知らない状況から問題を解こうとする。

判定者は答えを知っているアドバンテージがある。そして答えが正しいかの確認作業をする。

その確認作業が多項式時間で可能な問題は、探索者もまた必ず多項式時間で解けるかどうかというのが
pnp問題だったと思う。

v2の比較判定問題では特定のアルゴリズムは想定しておらず、一回にどれくらい判定可能なアルゴリズムなのかという抽象的な設定を置いている。

最も優れたアルゴリズムは一回の判定で解を得られるものである。
判定者が一回の判定で解を得られるアルゴリズムを探索者も使うことを想定する。

このとき単独判定問題と同様に、計算量オーダーの次元が異なっており、多項式時間で確認できる問題が問題の難しさに関係しているようには考えにくいという内容です。

具体的にはp.5　section　1.2.3 1:n 比較値を例に挙げると
判定者は「Fが最も重いか？」という入力に対して一回の判定でtureを出力するアルゴリズムを仮定する。
そのアルゴリズムを探索者が用いるのであるが解が不明なため、まず「Aが最も重いか？」という入力から行い、falseの出力を得る。次いでB、C・・・と判定してゆくことになる。

つまり判定者の計算量オーダーΟ(1)が、その次元を隔てた探索者の計算量オーダーに影響していないという印象を受けます。