あけましておめでとうございます。
忘れそうなので補足を書いておこうと思いますが、やる気がないのでざっくり。
この問題が難解なのは経路が非可換演算で構築されるためで、無限遠先までの経路について一元的な演算で表現することができないことにあると考えました。
論文の内容は
f：正規のコラッツ経路→行のコラッツ経路への写像という感じです。
なので数字のアップダウン→行のアップダウンで正規のコラッツ経路とは若干異なります。
大凡のイメージではアップダウンが等しければ省略して考えます。
枝のサイズが大きければ分岐数が多くなるので、増加数と減少数の合計は顕著になります。
両端で発散する経路の最小値が、仮にrow n →恒河沙で初めて登場したら
row n →那由他での1と接続する枝のサイズにまだ差がありますが、
row n →∞では枝のサイズの比率はほぼ同じになると考えられます。
僕が春先に考察していたことは帰納法で
ある部分にだけ注目すれば常に小さくなっていくとか、
また大小にとらわれず全ての数が接続されているのか調べるアプローチしていましたが、
全ての行が上手く埋まってくれませんでした。
またその行の埋まるパターンが非可換演算的ですと、大体の事が言えても無限遠先の正確な事まで分かりそうにないので、従来数学の規則性の範囲で行を埋めるパターンを探していた訳です。
いくらか前に見つけることはできたのですが、しばらく進展はしませんでした。
とりあえず投稿するに至りましたのでupしておきます。
証明を進めるにあたって、僕なり２つの行動に分けられると思いました。
一つは、どうしたら証明できるのだろうかという道筋を考察することです。
もう一つは、目的物を探すことです。
コラッツ予想に関して春先くらいに道筋をつけ、ずっと目的物を探しています。
探すだけなので特に深く考えることもなく、
ひたすら手を動かすだけなので退屈で地道な作業です。
何せ目的物があるのかもわからないのですから。
オー・アール・ゼットでした。無限の大きさを考慮してなかったようです。
またがんばります。
Collatz Problem V5を投稿しました。
1.4 増加率と減少率について
の検証
前回の記事まで非線形演算と呼称していものは、非可換演算の方が適当そうなので本項で改める。
非可換演算とは、新しい数学を形成するもので足し算と掛け算が混在して特定値を得ることが非常に困難である。
そこで3a+1を、3aとアバウトにすることで可換演算とする。
aを奇数の初項とすると計算は、a・3^m・2＾{-n}と単純化される。
ここで、できる限りYellow Chainを含む数列を仮定する。
Yellow Chainはm=n。
またYellow Chain(下線部)は有限回のステップで停止するのでk>2lとすると
a・3^m・2＾{-n} ・3^l・2＾{-k}・3^m・2＾{-n}・3^l・2＾{-k}・3^m・2＾{-n}・3^l・2＾{-k}・3^m・2＾{-n}・3^l・2＾{-k}………
経路を進むにつれて2＾{-1}の積の割合が増えていく。
増加率が小さくなっても初項aより数がまだ大きいが、減少率に転じると初項aより数が小さくなる。
しかし、どこまでも小さくなるのは実際と矛盾する。
これは非可換演算に戻すと4以下では+1が増加率として大きく影響しているからと考えられる。
増加率が限りなく小さくなるが減少率に転じない場合、経路は特定の値付近を振動することになるが
loopは途中に存在しないため、同じ経路を通らず振動し続けるのは不可能ではないかと考えているところです。
前回virsion.3まで分かったこと
・コラッツ経路はloopしない。
・yellow cellの連鎖は有限回で停止する。
しかし、「yellow cellの連鎖が有限回でもnot yellow cellを介せば数列が発散する可能性を排除できない。」という所まででした。
再考察してみたのですが、やはり非線形非可換であることがこの問題の障壁であると感じました。
そこで取るべき選択枝が2つ見えました。
一つ目は非線形非可換演算における証明を模索することです。
間も無く、このルートはかなり厳しいと推定されました。そもそも数学において非線形非可換演算の研究は日が浅く道具立てされていないという感もありましたが、例えば素数を見つける方法を言葉で表すと
2から始まる自然数列から初項を出力する→その初項の倍数を自然数列から取り除く
→その自然数列から初項を出力する→その初項の倍数を自然数列から取り除く→・・・
の繰り返しです。
コラッツ予想は偶奇に対しての分岐条件や2で何度割るかなど一貫してないため複雑であり、素数に関する問題ですら難解なので途方に暮れてしまいます。
二つ目は非線形非可換のなかに線形可換部分を見つけるという方法です。もしかしたら命題を解くにはそれで十分かもしないからです。
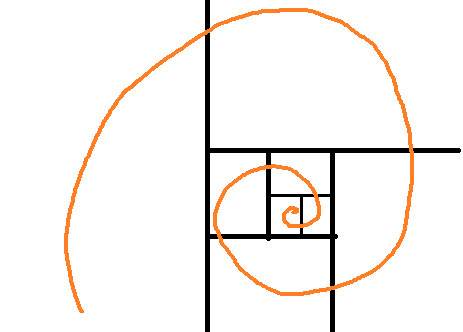
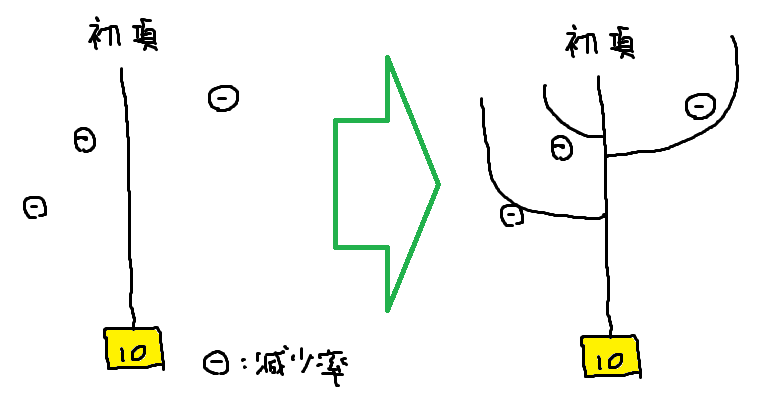
そのステップとして以下の経路に着目しました。色付きcellの逆路を進む場合を考えます。
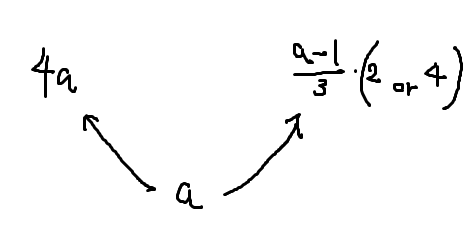
左の経路がnode-、右の経路は行を移動してからyellow または magenta cellへ移動する事を示しています。
次に任意の初項aから可能な限り左右交互に逆路を進んでいきます。
(下図の例で初項は34。下から上に進むのであって矢印の事でない。)
leefに突き当たる場合は、左の経路を進むということを繰り返します。すると紫の矢印で示した減少列があることがわかりました。
一見すると1へ収束しそうですが、22→34のようなyellow 2 chain(以上)あると減少列は停止してしまいます(magenta chainでは減少が続きます)。
非線形非可換の中に線形可換部分を見つけることできましたが、これに関して進展しませんでした。
証明のためには何より1へ収束しない数列の存在を否定することが条件であるので、その数列の構造について詳しく調べようと考えました。
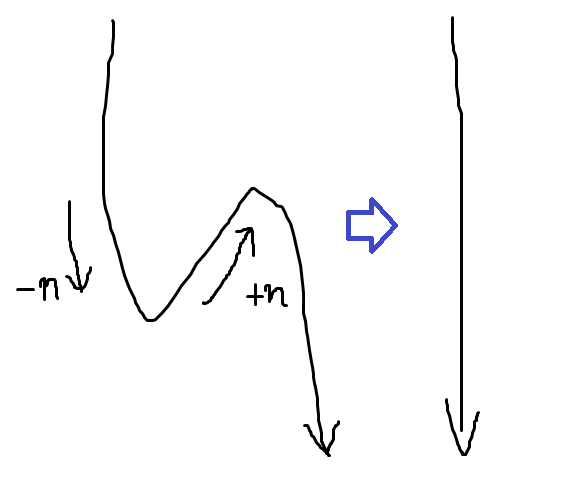
コラッツ経路の順路に関してyellow cellは数を増加、not yellow cellは数を減少させる性質があるのですが、逆路では関係性も逆になります。
上りn°の勾配は下りn°の勾配でもあるので、順路で増加率が大きいということは逆路では減少率が大きくなります。1へ収束する数列は順路では減少率が、逆路では増加率がnot yellow cellの方が一貫して大きいことで説明できます。
つまり、両端で発散する数列はyellow cellとnot yellow cellが最小値を挟んで増加率(または減少率)の優劣が逆転する数列になるという訳です。
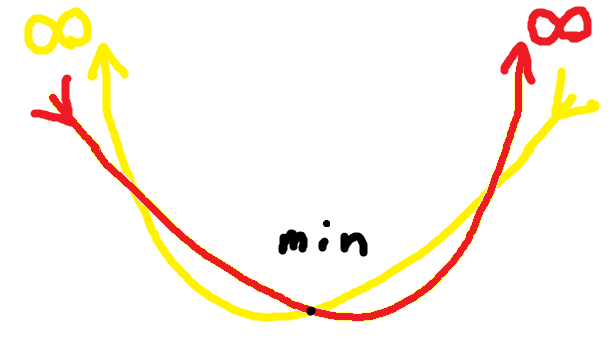
ここまでのコラッツ経路に対してのイメージはyellow cellによる数の増加、not yellow cellによる数の減少のせめぎ合いという抽象的な印象だけで、どちらかに軍配が上がるのかはさらに具体的に数値化して調べる必要があると考えました。
それから増加率・減少率に着目して計算すると必要な演算は掛け算・割り算のみであったため非線形という障壁はとりあえず壊すことができたようです。
ここからは論文virsion.4の補足説明していきます。
タイトルが内容と合わなくなったのでシンプルなものへ変更してます。
p.8 table 4：
yellow chainの出現頻度について調べてみた所、n chainは2^{n+1}周期ごとに出現することがわかりました。これはnot yellow cellの各初項の出現頻度に酷似してます。
そこで同周期に出現するyellow cellとnot yellow cellを対応させて増減率について計算してみるとmagentaの場合を除き減少率の方が大きい事がわかりました。
増加率(a)＜減少率(b)
※p.9で増加率=(減少率)^-1と定義してます。
また、出現率を分母に取るとyellow cellおよびnot yellow cellが現れる確率となります。
十分大きな初項では、table 6：1 chain & magenta の増加イベントが他の減少イベントにより打ち消され1へ収束しそうです。
しかし、これは独立試行の確率に基づいての考察であり証明することは不可能なのではないかと考え始めました。
独立試行とは前の試行が後の試行に影響を与えない確率の事を言います。
以前この確率に関して悩んだことがあり、うやむやになってたのでもう一度考察しました。
例えばサイコロの目の出る確率1/6は十分な回数の試行をしたときの各目の出る割合とも解釈できます。であれば「あまり出ない目は出やすくなるのだろう。」と以前考えてました。
サイコロ君が試行を記憶していてこんなことを思っているのでしょうか。
「しばらく3が出ていないな。そろそろ出してやるかなぁ。」
でもそれだと前の試行が後の試行に影響を与えていることになってしまいます。
シンプルな例をもう一つ。田中君がサイコロを振り、三回連続して5の目が出る確率を考えます。答えはもちろん1/6^3です。
では5の目が二回連続して出たところで斎藤君を呼んできて三回目の試行をします。三回目の試行で5の目出る確率は田中君にとっては1/6^3、斎藤君にとっては1/6になるのでしょうか。
立場によって確率が変わるというのもおかしな話です。
結論を言うと確率論は基本的に未確定な事象に適用するものということで説明できます。
つまり田中君がサイコロを一回も振ってない時点ならば三回連続して5の目が出る確率は1/6^3であり、
二回振った時点で次に5の目が出る確率は1×1×1/6となります。確定事象は1になるという答えを得れば当たり前だと感じます。
先の例は難しいですが、5の目が2回の事象で2回連続して出る確率と200回の事象で200回連続して出る確率は試行回数に対して反比例的であり、分母がとても大きくなる十分な試行回数に対して、連続して目が出る出ない事象等は相対的に些細な事象になるからと考えられます。
話を戻しますと、独立試行では限りなく100%に近くコラッツ数列が1へ収束することがわかったとしても、100%でないと証明したことにはならない数学の厳密さが要求されるからです。
しかし無数にある経路を一つ一つ調べ上げるのは無理があるので、やはり確率でアプローチするしかなさそうです。このジレンマは解消できないと思った矢先、従属試行なら道が開けるのではないかと考えました。(この時点で独立・従属試行という言葉はわからず調べました。)
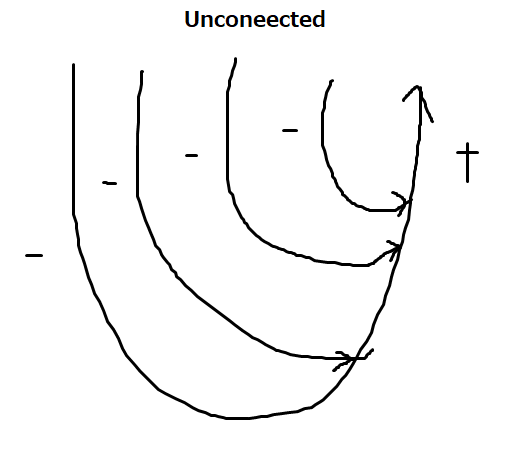
従属試行とは独立試行の反対で前の試行が後の試行に影響を与える確率の事を言います。例によってサイコロを振る場合、既に出た目はノーカウントとすると、確率の過程は
1/6×1/5×1/4×1/3×1/2×1
であり六回の試行に制限され、最後の確率は1であると断定できます。何回でも同じ目が出る可能性がある独立試行とは明らかに異なっている点です。
コラッツ数列はloopが存在せず、また図に示したような青と赤の重複してない経路があるので従属試行が適用できそうです。
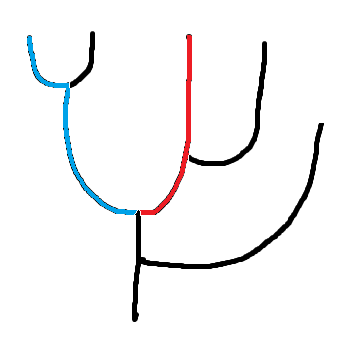
p.11の説明：
実際のコラッツ経路ではloopが存在せず同じ経路は通らないため重複cellを除く必要があります。
例えばnode+でred cell 352が出現すると必然的にnode-においてcyan cell 88が出現するので、node+でcyan cell 88が出現する確率は0になります。
これを考慮して重複cellを除いたもの(Aは増加率、Bは減少率)がtable 11になります。
table 12ではyellow cellを初項(y初項)としてますが便宜的なものです。（論文中では初項および終点をyellow cellにしてます。）
y初項に対して、その初項以下の全てのイベントを掛け合わせたもの(増加率累計)がy期待値(yellow cellの終点)となります。
論文に示してないですが16、64、256…の部分にはnot yellow cellは実際には存在しないので16には16周期のgreen、64には64周期のblueイベントを一つ余分にカウントしています。そのため24.08…×3.48、2.96…×3.48、0.04…×13.94として取り除きます。magentaのあるnode-に属するnot yellow cellの初項の出現が一つずれる補正をしてます。
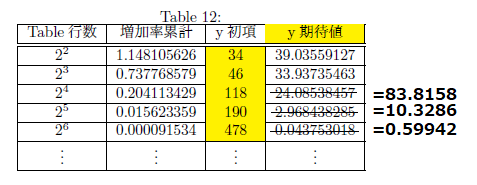
y期待値はTable行数が増えるにつれて減少傾向にあることがわかります。
実際の経路は初項以下の全イベントが出現するものではないのでy期待値の意味するところが不明瞭です。そこで近い条件から考えてみました。
1へ収束するとわかっている数列では、その最大値を初項とすればその初項以下のイベントのみ出現します。27が初項ならnodeの最大値9232を初項とします。この初項における期待値として考えれば少々理解できます。では最大値を設定できない1へ収束するかわからない条件ではどうなのでしょうか。
Table行数が2^6以上の任意の初項であれば1へ収束する期待値を有していると推測できます。その理由としてyellow cellの最小値は10であり期待値がそれ以下である点が挙げられます。
ところで実際の経路ではyellow cellが10より小さくなることはなく、減少率(yellow cellも含む減少イベント)が余ってしまうので奇妙な感じがしました。これについて実際の経路は一本ではなく枝分かれしているからだと考えています。
一方、期待値が10より大きくなるTable行数2^6以下では、初項がその(初項までの)範囲のイベントだけで1へ収束できるものが少ないと解釈できます。実際にはTable行数2^6以上の余った減少イベントによって1へ収束しているものと考えれます。またTable行数2^6以下の初項の数は有限なので十分大きな任意の初項であれば、いずれもy期待値は10以下を示し収束する余力ありと推測されます。
ここで、両端で発散する数列が存在する場合について考察します。
両端で発散する数列が一つでも見つかると、その逆路を進めば(leefもありますが、ｐ.4より埋め尽くされていないことは判明しているので)枝分かれして経路が増えていきます。
図に示した赤丸印は両端で発散する数列全体の最小値です。その最小値を通らない経路もありますので各数列の最小値(ピンクの丸印)もあることがわかります。
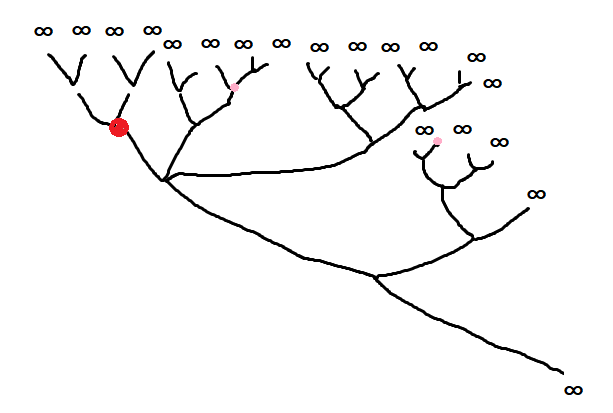
P.2の下【Collatz tree の組立て方】の手順による動線イメージが以下の図になります。
行を下にずっと進んでいきますと、まず両端で発散する数列の全体の最小値に遭遇します。次いで各数列の最小値に遭遇します。
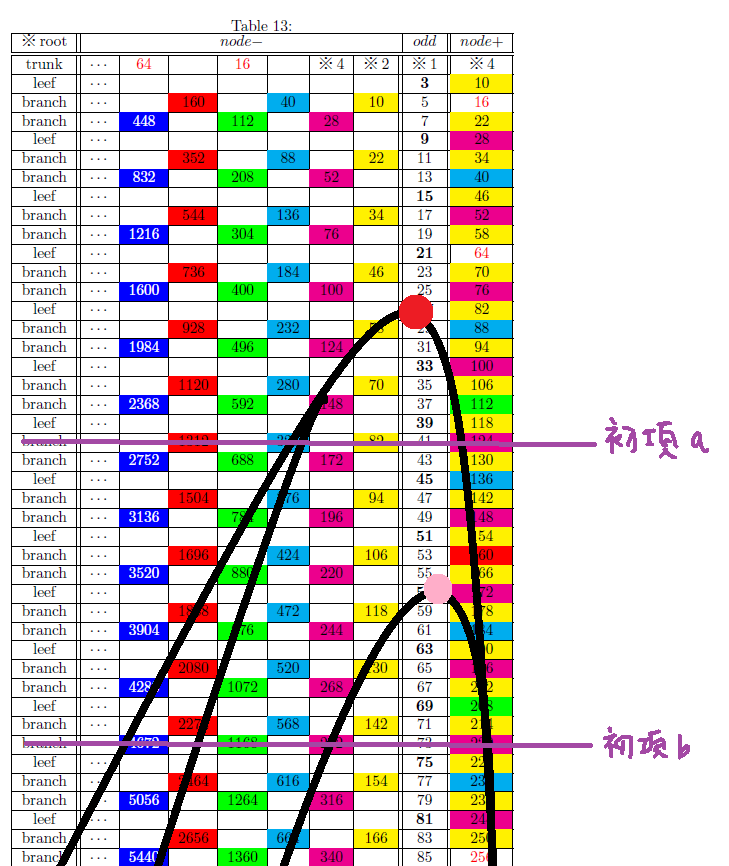
両端で発散する数列は1へ収束しないので、任意の初項を超えていく経路数は初項が大きいほど増えていきます。
収束しない経路数が増加すると先の説明と同様、初項までの範囲における減少率(yellow cellも含む減少イベント)は余るので1へ収束する経路数が増えると考えられます。
従属試行の観点から、任意の初項のy期待値はいずれも収束の余力ありと推定できるので、収束しない数列が存在すれば、その分、収束する経路数を増えるので両端で発散する数列の経路数は増加傾向にはならないのではないかと推測されます。
しかし両端で発散する数列が存在するならば初項が大きくなるにつれて経路数が増加するので、排反事象でありえないのではないかという説明をProof 11に書いてます。
途中から、ざっくりとした考察なのですが取り敢えずこんなところです。
あれからコラッツ予想に関して幾分進展がありました。イエローの事ばかり考えているのでイチローがイエローに見えてきます。イチローの打率が加齢とともに小さくなる事とは関係ないですが、確率的な見解を脱する事ができず証明したことにはなりません。もう少し頑張っても無理そうだったら、そこまでの論文予定しております。
最近コラッツ予想についてずっと考えている。イエローsellの事ばかり頭から離れず、今日は駅の中で点字ブロックがイエローsellに見えて何だかコラッツ経路の中を歩いているように感じた。
偶然か今日が点字ブロックの日だと知り日記を書いておこうと思った。以上
ふとコラッツ予想について考えてみたところ、若干の進展がありました。
2周期のセルの連鎖は有限回で停止するというものです。しかし手順3の2周期でないセルを介して連鎖が継続する可能性が残されています。
ところで「こらっつよそう」を変換したら「こらっ強そう」と出ました。本当に手ごわそうです。
記事が滞っているので非線形について改めて考えてみます。正確な定義とは異なるかもしれません。
投稿したコラッツ論文のintroductionに、この問題は非線形な部分があり証明が困難であると記述しました。
ループに関しては論理的な説明により非線形な部分を回避できたような気がします。
【コラッツ問題とは】
「任意の自然数を初期値として奇数ならば3を掛けて1を加え、偶数ならば2で割る。この試行により必ず1に到達する。」というものである。この演算は非線形であると考えられる。
1から100までの和は少年期のガウスの計算法が有名であり
1 +2 +3+…+98 +99 +100
+ ）100 +99 +98+… +3 +2 +1
101+101+101+…+101+101+101
101が100項あるため、1から100までの和は (101×100)/2=5050
よって1からnまでの和の一般解は (n(n+1))/2であり、これは線形である。
では線形と非線形の違いとは何かと言えば、函数において入出力間に演算順序の制限という概念が存在するか否かという事である。（物理的にはエントロピー等の時間に関係していると予想しています。）
上記(n(n+1))/2はnを入力すれば、1からnまでの和が出力されるが演算のステップとしては一回で終了する。一方、コラッツ問題の演算ではステップを複数回を要する。このような非線形およびフラクタルを形成する背景には演算順序の制限とその反復計算が第五の演算子となっているためである。
【非線形をつくる第五の演算子とは】
具体的には四則演算子に加減乗除（＋－×÷）があるが、加減と乗除の混合式では演算の順序に制限が伴う。これにより前の演算ステップを基底として次の演算を重ねるものである。ただし全くの不規則な演算では非線形の概念は不明瞭であるため何らかの規則的な演算を行う。
(※非線形演算であっても線形に帰着されるものがないとは限らない。)
身近な例としてはルービックキューブが挙げられる。
各面の色が揃っている状態からシャッフルを行う。ビデオを逆再生するように逆シャッフルを行えば当然、色が揃った状態に戻すことができる。しかし逆シャッフルの順序を変えてしまうと元の状態には原則戻ることはない。
これが非線形の演算が困難な理由である。(線形演算ができないので困難)
コラッツ問題は、さらに条件関数「～ならば」が伴うため数学者ポール・エルデシュが「数学はまだこの種の問題に対する用意ができていない」と述べた理由が分かる。
shitetsuronnkou blog 